
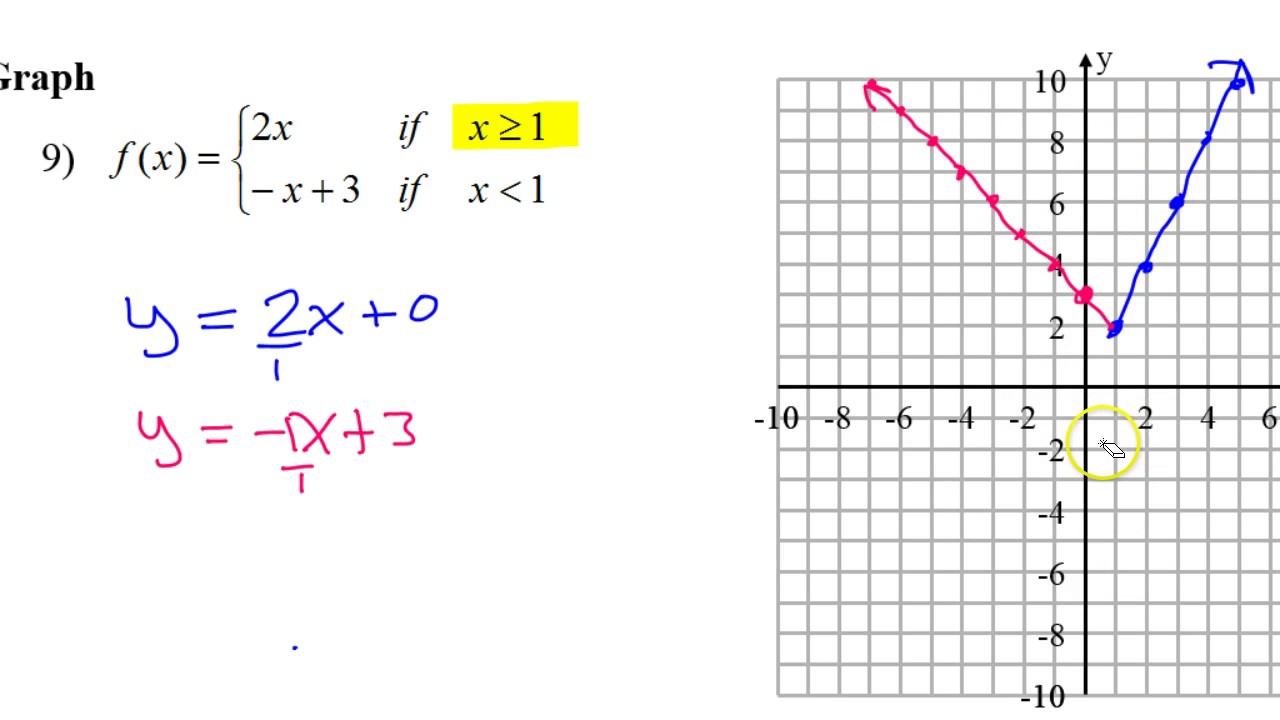
Instead of being defined over all Real values of x, they start and stop at specific values. These graphs do not seem to follow all the rules you were taught for graphing lines or parabolas. And the green line stops at x = 5.5, just as it reaches the horizontal axis. And when x = 3 the blue parabola turns into a green line with a very different slope. It does not appear of the left of the vertical axis at all. In the graph on the right, note that the blue curve starts at x = 0. Furthermore, when x = 3 the blue line stops and the green line begins – but with a different slope. It does not appear to the left of the origin at all. In the graph on the left, note that the blue line starts at the origin. Two examples of such situations could be: The behavior being described might start at a specific time, or its nature changes at one or more points in time. \(\displaystyle f\left( x \right)=\left\\) graph, we can just use a closed circle as if it appears on both functions.While many relationships in our world can be described using a single mathematical function or relation, there are also many that require either more or less than what one equation describes. Note that there is an example of a piecewise function’s inverse here in the Inverses of Functions section. Thus, the \(y\)’s are defined differently, depending on the intervals where the \(x\)’s are. The easiest way to think of them is if you drew more than one function on a graph, and you just erased parts of the functions where they aren’t supposed to be (along the \(x\)’s). Piecewise functions (or piece-wise functions) are just what they are named: pieces of different functions (sub-functions) all on one graph. Obtaining Equations from Piecewise Function Graphs
#PIECEWISE FUNCTION HOW TO#
How to Tell if a Piecewise Function is Continuous or Non-Continuous Applications of Integration: Area and Volume.Exponential and Logarithmic Integration.Riemann Sums and Area by Limit Definition.Differential Equations and Slope Fields.Antiderivatives and Indefinite Integration, including Trig Integration.Derivatives and Integrals of Inverse Trig Functions.Exponential and Logarithmic Differentiation.Differentials, Linear Approximation, and Error Propagation.Curve Sketching, including Rolle’s Theorem and Mean Value Theorem.Implicit Differentiation and Related Rates.Equation of the Tangent Line, Tangent Line Approximation, and Rates of Change.Basic Differentiation Rules: Constant, Power, Product, Quotient, and Trig Rules.

Differential Calculus Quick Study Guide.


 0 kommentar(er)
0 kommentar(er)
